賭徒迷信的是運(yùn)氣，
何鴻燊相信的是數(shù)學(xué)。

01 

   賭王何鴻燊

   2020年5月26日，賭王何鴻燊逝世，享年98歲。

   這一天中午，港澳地區(qū)突降大雨。

   這位知名的港澳企業(yè)家，素有“澳門(mén)賭王”之稱(chēng)的傳奇人物，至此謝幕。

   1961年，澳葡政府規(guī)定博彩業(yè)須通過(guò)專(zhuān)營(yíng)制度實(shí)施。

 
   何鴻燊看準(zhǔn)時(shí)機(jī)，接手葡京賭場(chǎng)，從此事業(yè)蒸蒸日上。

 
   直至今日，何鴻燊及其家族控制著高達(dá)5000億港元的資產(chǎn)。 

 

▲何鴻燊

   曾有人請(qǐng)教何鴻燊：“如果他們老是贏怎么辦？”

 
   老爺子說(shuō)過(guò)一句名言：“不怕你贏,就怕你不來(lái)?！?

   在何鴻燊的眼中，他是不可能輸?shù)摹?

 
   因?yàn)樗€的不是運(yùn)氣，而是數(shù)學(xué)。

   一個(gè)現(xiàn)代的賭場(chǎng)，它集中了概率學(xué)、統(tǒng)計(jì)學(xué)等諸多知識(shí)。

   所謂的各種致勝絕技，除了《賭圣》里的周星馳，現(xiàn)實(shí)世界里的周潤(rùn)發(fā)都不信。

   一個(gè)癡迷于發(fā)財(cái)夢(mèng)的賭徒永遠(yuǎn)不明白，與自己對(duì)賭的不是運(yùn)氣，也不是莊家，而是狄利克雷、伯努利、高斯、納什、凱利這樣的數(shù)學(xué)大師，贏的概率能有多大？

02

看得到的是概率
看不見(jiàn)的是陷阱

   何鴻燊的記憶力和算力一直堪稱(chēng)神奇，

 
   他創(chuàng)業(yè)期間，澳門(mén)的兩千多個(gè)電話(huà)號(hào)碼，他能倒背如流。

 
   直接比復(fù)雜的賭博游戲，在數(shù)學(xué)上可能比不過(guò)。

 
   就來(lái)一個(gè)最簡(jiǎn)單的玩法：與何鴻燊比拋硬幣。

   規(guī)則是這樣的：

   擲硬幣，正面贏反面輸，如果你贏了可以拿走比賭注多一倍的錢(qián)，如果輸了則會(huì)賠掉本金。

 
   你一聽(tīng)可能覺(jué)得這游戲還不錯(cuò)，公平！

   于是你拿出了身上的100元來(lái)玩這個(gè)游戲，每次下注5元，這樣你至少有20次的下注機(jī)會(huì)。

   不過(guò)，你運(yùn)氣不太好，第一把就是反面，輸了5塊錢(qián)。

 
   生性樂(lè)觀的你覺(jué)得沒(méi)什么，反正不管怎么說(shuō)，贏面都有50%，下一把就可以贏回來(lái)。
   結(jié)果，很快你就把身上的錢(qián)都輸光了。

 

   你百思不得其解，明明是公平的50%贏面，在50%概率下至少不會(huì)虧本的，可為什么最后會(huì)輸光？

   事實(shí)上，你以為自己看到了50%的概率，把游戲看得透徹明白，殊不知，你看到了概率，卻沒(méi)有看到背后的陷阱：大數(shù)定律。

03

大數(shù)定律

   你覺(jué)得游戲是公平的：

   一正一反，均為50%概率，按照大數(shù)定律來(lái)說(shuō)，這是必然規(guī)律。

 
然而，你有沒(méi)有想過(guò)，正是這種你以為的“公平”，讓你誤解了大數(shù)定律，才陷入了“賭徒謬論”里呢？

   先來(lái)看看這種讓你覺(jué)得“公平”的大數(shù)定律究竟是什么。

 
   它是數(shù)學(xué)家伯努利提出的：

   假設(shè)n是N次獨(dú)立重復(fù)試驗(yàn)中事件A發(fā)生的次數(shù)，p是每一次試驗(yàn)中A發(fā)生的概率，那么，當(dāng)N趨于無(wú)窮時(shí)：

 

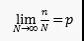
   式中n表示發(fā)生次數(shù)，N表示試驗(yàn)總次數(shù)。

   也就是說(shuō)，大量重復(fù)的隨機(jī)現(xiàn)象里其實(shí)藏著某種必然規(guī)律。

還是以擲硬幣為例，當(dāng)投擲次數(shù)足夠大時(shí)，出現(xiàn)正（反）面的頻率將逐漸接近于1/2，且隨著投擲次數(shù)的增加，偏差會(huì)越來(lái)越小，如下圖。這是最早發(fā)現(xiàn)的大數(shù)定律之一。

▲擲硬幣頻率分布圖

   從表面概率看，這確實(shí)是場(chǎng)公平的游戲。

 
   但這種公平是有一定條件的，注意，這就是普通人看不到的。

   大數(shù)定律講究“大量重復(fù)的隨機(jī)現(xiàn)象”，只有足夠多次試驗(yàn)才能使得硬幣正反面出現(xiàn)次數(shù)與總次數(shù)之比幾乎等于1/2。

   可具體多少次才算“足夠多”？才能夠把它用在個(gè)人對(duì)賭上？

沒(méi)有人知道。因?yàn)?，概率論給出的答案是——無(wú)窮大。誰(shuí)也不知道無(wú)窮大有多大，只知道這是一個(gè)令人仰望的數(shù)量。

   可投擲硬幣次數(shù)越小，大數(shù)定律的身影就越模糊，可能10次中5正5反，也可能9正1反，也可能10正0反或0正10反……

   現(xiàn)實(shí)往往是，在遠(yuǎn)未達(dá)到“足夠多”次試驗(yàn)時(shí)，你就已經(jīng)輸了個(gè)精光了。

 
   你覺(jué)得自己比何鴻燊更有錢(qián)嗎？

   你身上有100元結(jié)果如此，你身上有10000元結(jié)果也是如此，就算你身上有一百萬(wàn)也是如此，因?yàn)槟阌肋h(yuǎn)不可能有“足夠多”。

   “輸贏概率為50%”，這本身就具有很大的誤導(dǎo)性。在硬幣拋出之前，50%的概率代表的是可能性；在硬幣拋出之后，50%代表的是結(jié)果的統(tǒng)計(jì)平均值，卻并不是實(shí)際分布值。

   這是你對(duì)大數(shù)定律的誤解之一。

   把“大數(shù)定律”當(dāng)“小數(shù)定律”，覺(jué)得游戲是無(wú)條件“公平”的，正面和反面出現(xiàn)的頻率都為1/2。
   這種在潛意識(shí)里被奉為圭臬的“公平”，緊接著讓你踏入了第二個(gè)誤解——“賭徒謬論”。

04

賭徒謬論

   大數(shù)定律有一個(gè)明顯的潛臺(tái)詞：

   當(dāng)隨機(jī)事件發(fā)生的次數(shù)足夠多時(shí)，發(fā)生的頻率便趨近于預(yù)期的概率。但人們常常錯(cuò)誤地理解為：隨機(jī)意味著均勻。

   如果過(guò)去一段時(shí)間內(nèi)發(fā)生的事件不均勻，大家就會(huì)“人工”地從心理上把未來(lái)的事情“抹平”。也就是，如果輸了第一把，那下一把的贏面就會(huì)更大。

   這種你下一把就可以贏回來(lái)的強(qiáng)烈錯(cuò)覺(jué)，就是“賭徒謬論”。

 

   當(dāng)你玩游戲連輸時(shí)，你的心底突然冒出一個(gè)神秘的聲音，它激動(dòng)地朝你吶喊：穩(wěn)住，風(fēng)水輪流轉(zhuǎn)，下一把你很有可能就要贏了何鴻燊！

   而其實(shí)，上一把和下一把之間并沒(méi)有任何聯(lián)系。

   就好比一個(gè)笑話(huà)：

   在乘坐飛機(jī)時(shí)帶著一枚炸彈就不會(huì)遇上恐怖分子了，因?yàn)橥患茱w機(jī)上有兩枚炸彈的可能性是極小的。

   兩者如出一轍，都把獨(dú)立事件誤認(rèn)為是互相關(guān)聯(lián)的事件。

 
   要知道，大數(shù)定律的工作機(jī)制，可不是為了平衡對(duì)抗。

   在這場(chǎng)游戲中，任意兩次事件之間并不會(huì)相互產(chǎn)生影響。

 
賭局是沒(méi)有記憶的，哪怕你曾經(jīng)輸了多次，它也不會(huì)因此給你更多勝出的機(jī)會(huì)。

05

只要進(jìn)了賭場(chǎng)
你就是一個(gè)窮鬼

   你不服，想與何鴻燊再來(lái)一把。

 
   游戲仍然很簡(jiǎn)單：還是拋硬幣。

   何鴻燊沒(méi)有別的要求，這次你要來(lái)他的賭場(chǎng)賭。

   規(guī)則還和前面一樣：擲硬幣，正面贏反面輸，如果你贏了可以贏走比賭注多一倍的錢(qián)，如果輸了則會(huì)賠掉本金。

   這一次你運(yùn)氣很不錯(cuò)，第一把你就贏了何鴻燊100元！可把你高興壞了！

 
   但是和前面的個(gè)人對(duì)賭相比，這次多了一個(gè)賭場(chǎng)。

   賭場(chǎng)跟你說(shuō)：“你看你也贏了這么多，我呢，辛辛苦苦搭個(gè)場(chǎng)子，最后什么都沒(méi)撈著。要不這樣，你贏了，就給我留下2%當(dāng)流水，就算是救濟(jì)救濟(jì)老哥，給捧捧場(chǎng)！”

   你想了下，2%也不多，拿去吧，不差錢(qián)！好了，這事就這么定下來(lái)了。

   然而你做夢(mèng)都想不到的是：就是這小小的2%，又一次讓你輸?shù)脙A家蕩產(chǎn)！

   你同樣百思不得其解，不過(guò)是小小的2%抽水，毫不起眼，明明也是開(kāi)門(mén)紅，玩了很多把，贏了不少，可為什么在最后，它就成為了莊家賺錢(qián)的利器，自己又輸光了？

   天真的你，肯定不知道在賭場(chǎng)有一個(gè)逃不開(kāi)的魔咒：賭徒破產(chǎn)困境。

06

賭徒破產(chǎn)困境

   一鼓作氣，鴻運(yùn)當(dāng)頭。

   第1把，贏；第2把，贏；第3把……

   你覺(jué)得自己被幸運(yùn)女神眷顧，一身富貴命。

   可早在18世紀(jì)初，那群熱愛(ài)賭博的概率論數(shù)學(xué)家們，就提出了那個(gè)讓賭徒聞風(fēng)喪膽的破產(chǎn)噩夢(mèng)：
在“公平”的賭博中，任何一個(gè)擁有有限賭本的賭徒，只要長(zhǎng)期賭下去，必然有一天會(huì)輸個(gè)精光。

   我們來(lái)看看，為什么那么多長(zhǎng)期賭徒都輸成了窮光蛋？錢(qián)都到哪去了？

   假如你的小金庫(kù)是r，你帶著小金庫(kù)和莊家開(kāi)始了一場(chǎng)追逐多巴胺刺激的賭博游戲，打算贏得s后就離開(kāi)，每一局你贏得籌碼的概率為p，那你輸光小金庫(kù)的概率有多大呢？

   我們可以在馬爾科夫鏈、二項(xiàng)分布、遞推公式等的助攻下，列出一組組粗暴的、令人頭皮發(fā)麻的函數(shù)。

 

   它形象地揭示了賭徒輸光定理的含義：所謂的“公平”賭博，其實(shí)并不公平。

   在f(r,n)中，隨著次數(shù)n的增加，賭徒輸光的概率會(huì)逐漸增加并趨近于1，并且r越小，這種趨勢(shì)越明顯。這說(shuō)明在公平賭博的情況下，擁有籌碼更少的賭徒會(huì)更容易破產(chǎn)。

   而在f(r,s,p)中，以一種冷峻而無(wú)情的話(huà)語(yǔ)告訴我們：如果希望輸光的概率比較小，那么需要每次的贏面p足夠大或者是手里的籌碼r足夠多。

   你真能從莊家那里虎口奪食、在贏面和籌碼中PK一把嗎？

 
   答案，顯然是難乎其難的。

  第一，莊家不是賭徒。

   莊家的背后是賭場(chǎng)，也就意味著莊家相比于你，擁有“無(wú)限財(cái)富”。你的小金庫(kù)永遠(yuǎn)比不過(guò)莊家的賭場(chǎng)錢(qián)莊，這也意味著，你比莊家更容易山窮水盡。

   當(dāng)然，也許你家里有礦，壕到一擲千金，壕到家產(chǎn)超過(guò)5000億。

   但超級(jí)賭場(chǎng)也會(huì)設(shè)置最大投注額，這并不是他們好心，想保護(hù)你免遭破產(chǎn)，他們只是為了自保才設(shè)計(jì)了一道安全屏障，來(lái)抵抗“無(wú)限財(cái)富”帶來(lái)的破產(chǎn)威脅。畢竟萬(wàn)一哪天比爾蓋茨去賭場(chǎng)找樂(lè)子，一次性砸個(gè)幾百億進(jìn)去，那賭場(chǎng)老板恐怕真的要哭了。 

   第二，莊家是“抽水”收入。

   忘了拋幣游戲中那毫不起眼的2%了嗎？賭徒贏錢(qián)后，莊家會(huì)從賭徒手中抽取一定比例的流水傭金。
   這樣一來(lái)，即使你有一個(gè)小金庫(kù)足以和莊家慢慢磨，打一場(chǎng)持久戰(zhàn)，但贏得越多，為莊家送去的“抽水”越多。長(zhǎng)此以往，你還是輸了，錢(qián)都進(jìn)了莊家的口袋。

   最終，莊家賺的錢(qián)只跟賭徒下注大小有關(guān)。

   你還是難以逃開(kāi)那個(gè)牢籠般的魔咒，一步一步，走向了兩袖清風(fēng)、空空如也的境地。

 
   這世上，天才終究是少數(shù)，而“賭神”、“賭王”之所以成為普通賭徒難以望其項(xiàng)背的存在，不僅因?yàn)樗麄兩钪O賭徒心理，也不僅因?yàn)樗麄兌€場(chǎng)規(guī)則，更因?yàn)樗麄兌迷撓伦⒍嗌佟?

07

賭王的眼中只有“窮鬼”

   在賭王何鴻燊的眼里，世界上或許只有兩種人：

 
   一種現(xiàn)在是窮鬼，一種未來(lái)是窮鬼。

   但有時(shí)賭場(chǎng)老板也會(huì)有所忌憚，特別是遇到善用數(shù)學(xué)博弈的高手之時(shí)。

 
   其中，凱利公式在高級(jí)賭徒的世界里大名鼎鼎，是頂級(jí)高手常用的數(shù)學(xué)利器。

 
   它也是賭場(chǎng)老板最擔(dān)心被暴露的賭場(chǎng)秘密。 

   那什么是凱利公式，我們先看一個(gè)例子：

 
   一個(gè)1賠2（不包括本金）的簡(jiǎn)單賭局，扔硬幣下注，假設(shè)賭注為1元，硬幣如果為正面則凈贏2元，如果為反面則輸?shù)?元?，F(xiàn)在你的總資產(chǎn)為100元，每一次的押注都可投入任意金額。

   你會(huì)怎么賭呢？已知擲硬幣后正反面的概率都為50%，賠率是1賠2（不包括本金），那么這個(gè)賭局其實(shí)只要耐心不斷地去下注，再拋開(kāi)不公平因素的干擾，幾乎就能賺。

   因?yàn)閿S硬幣次數(shù)越多，其正反面出現(xiàn)概率就越會(huì)穩(wěn)定在50%，收益2倍，損失卻只是1倍，從數(shù)學(xué)上講那是穩(wěn)賺不賠的賭局。

   但實(shí)際情況卻可能會(huì)有偏差。

   如果你是冒險(xiǎn)主義者

   你可能會(huì)想，要玩就玩票大的，All In！一次性把100元全押上，幸運(yùn)的話(huà)，一次正面就可以獲得200元，又是一段值得炫耀的賭史。

   可是，如果輸了，得把100元資產(chǎn)拱手獻(xiàn)給對(duì)方，你就一無(wú)所有。好不容易來(lái)趟拉斯維加斯，這肯定不是明策。

   如果你是保守主義者

   你可能會(huì)想，謹(jǐn)慎點(diǎn)，百分之一慢慢來(lái)。

 
   你每次只下注1元，正面贏2元，反面輸1元。

   玩了20把突然覺(jué)得，對(duì)方下注10元一次就贏得20元，自己1次才贏2元、10次才能贏得20元，感覺(jué)自己已經(jīng)錯(cuò)過(guò)幾個(gè)億而開(kāi)始后悔！

   那到底該以多少比例下注才能獲得最大收益呢？

 
   普通賭徒一般一臉茫然，但凱利公式卻能夠告訴我們答案：

 
   計(jì)算后每次下注比例為當(dāng)時(shí)總資金的25%，這樣就能獲得最大收益。

08

賭場(chǎng)大BOSS：凱利公式

   在公式中，各參數(shù)意義為：

 
   f= 應(yīng)投注的資本比例；

 
   p = 獲勝的概率（也就是拋硬幣正面的概率）；

 
   q = 失敗的概率，即(1 - p)（也就是硬幣反面的概率）；

 
   b = 賠率，等于期望盈利 ÷可能虧損（也就是盈虧比）；

 
   公式上面的分子(bp-q)代表“贏面”，數(shù)學(xué)中叫“期望值”。

   什么才是不多不少的合適賭注呢？凱利告訴我們要通過(guò)選擇最佳投注比例，才能長(zhǎng)期獲得最高盈利。
   回到前面提到的例子中，硬幣拋出正反面的概率都是50%，所以p、q獲勝失敗的概率都為0.5，而賠率＝期望盈利÷可能虧損=2元盈利÷1元虧損，賠率就是2，我們要求的答案是f，也就是(bp - q) ÷ b = (2 * 50% - 50%) ÷ 2 = 25%。

   由此，我們根據(jù)凱利公式的計(jì)算而得投注比例，每次都拿出當(dāng)前手中資金的25%來(lái)進(jìn)行下注。設(shè)初始資金為100，硬幣為正面時(shí)收益為投注的2倍，為反面則失去投注金額。在下表中，我們模擬計(jì)算了10次賭局的收益情況。

   ▲表1-25%投注下10次收益表

   ▲表2-25%投注下10次收益表

   表1從先正后反的情況計(jì)算了收益，而表2則計(jì)算了正反分布交錯(cuò)情況下的收益結(jié)果。

 
   比較兩表，我們最終可以發(fā)現(xiàn)其收益是相等的，硬幣出現(xiàn)正反面的先后順序?qū)τ谧罱K收益的計(jì)算結(jié)果并無(wú)影響。

   而按25%的投注比例進(jìn)行投注，收益基本呈現(xiàn)穩(wěn)步增長(zhǎng)的大趨勢(shì)。

 
   但假設(shè)投注比例為100%時(shí)，10次當(dāng)中只要出現(xiàn)任意一次的反面，就會(huì)徹底輸光身上的所有錢(qián)，直接出局，且每輪反面概率還為50%。 

   而每次1元1元地投注，也就是投注比例為1%的時(shí)候，10次數(shù)學(xué)上的收益為100+10×50%×2+(-1)×10×50%=105，這風(fēng)險(xiǎn)很小，不過(guò)收益太低。由此看來(lái)，凱利公式才是最大的贏家。

   賭場(chǎng)操盤(pán)者每一次下注的時(shí)候，都會(huì)謹(jǐn)記數(shù)學(xué)原則；而作為普通賭徒，除了心中默念“菩薩保佑”外，哪里知道這后面的數(shù)學(xué)知識(shí)。

   所以，就算你贏得了財(cái)神爺?shù)闹С郑阋灿肋h(yuǎn)贏不了“凱利公式”。

09

除非100%贏 
否則任何時(shí)候都不應(yīng)下注

   所有的賭場(chǎng)游戲，幾乎都是對(duì)賭徒不公平的游戲。

 
   但這種不公平并非是莊家出老千，現(xiàn)代賭場(chǎng)光明正大地依靠數(shù)學(xué)規(guī)則賺取利潤(rùn)，從某種意義上來(lái)講，賭場(chǎng)是最透明公開(kāi)的場(chǎng)所。

   如果不是這樣，進(jìn)出賭場(chǎng)不知有多少亡命之徒，何鴻燊哪怕九條命都不夠，遑論活到98歲。
凱利公式不是憑空設(shè)想出來(lái)的，這個(gè)數(shù)學(xué)模型已經(jīng)在華爾街得到了驗(yàn)證，除了在賭場(chǎng)被奉為“勝利理論”，同時(shí)也被稱(chēng)為“資金管理神器”，它是比爾格羅斯等投資大佬的心頭之愛(ài)，巴菲特依靠這個(gè)公式也賺了不少銀子。

   回歸到賭場(chǎng)討論這個(gè)公式，根據(jù)f=(bp-q)/b公式結(jié)論，期望值(bp-q)為負(fù)時(shí)，賭徒不具備任何優(yōu)勢(shì)，也不應(yīng)下任何賭注。

   賭博這種游戲，要下負(fù)賭注，你不如自己開(kāi)個(gè)賭場(chǎng)當(dāng)莊家。

   世界上有為數(shù)不多的“賭神”，他們當(dāng)中有信息論的發(fā)明者香農(nóng)，數(shù)學(xué)家愛(ài)德華·索普等，他們通過(guò)一系列復(fù)雜的計(jì)算和艱深的數(shù)學(xué)理論，把某些賭戲的贏率扳回到50%以上，例如21點(diǎn)靠強(qiáng)大的心算能力可以把概率拉上去。

   但就憑你讀書(shū)時(shí)上課打瞌睡、輸了只知道倍投翻本的可憐知識(shí)，以及九九乘法表的那點(diǎn)算力，還是先老實(shí)讀完以下3條準(zhǔn)則。

   ①期望值(bp-q)為0時(shí)，賭局為公平游戲，這時(shí)不應(yīng)下任何賭注。

   ②期望值(bp-q)為負(fù)時(shí)，賭徒處于劣勢(shì)，更不應(yīng)下任何賭注。

   ③期望值(bp-q)為正時(shí)，這時(shí)按照凱利公式投注賺錢(qián)最快，風(fēng)險(xiǎn)最小。

   其實(shí)最終結(jié)論只有一個(gè)：除非100%贏，否則任何時(shí)候都別賭上全部身家，即使贏率相對(duì)較高也要謹(jǐn)慎。

10

贏得勝利的唯一法則：不賭

   有人可能說(shuō)，我又不是與何鴻燊對(duì)賭，我只要贏了對(duì)手就行了。

 
   可無(wú)論是你還是對(duì)方，贏者都是要給賭場(chǎng)“流水”的，賭的時(shí)間一長(zhǎng)，兩者都是在給賭場(chǎng)打工。

   現(xiàn)代賭場(chǎng)自己做莊的可能性很小，他們更依賴(lài)數(shù)學(xué)定理來(lái)自己獲取利益。

 
   賭王何鴻燊的數(shù)學(xué)到底怎么樣，沒(méi)人知道。

   只知他的兒子何猷君，從小就是數(shù)學(xué)天才，MIT史上最年輕金融碩士，連續(xù)兩年在“世界數(shù)學(xué)測(cè)試”邀請(qǐng)賽中獲獎(jiǎng)。

   沒(méi)有誰(shuí)能說(shuō)服一個(gè)墮落的賭徒，因?yàn)檫@是人格的缺陷。

 
   但如果你還是一個(gè)具有理性精神的人，就別再迷戀所謂的運(yùn)氣。

   賭徒能夠依靠的是祖宗保佑，而賭場(chǎng)后面的大佬是高斯、凱利、伯努利這樣的數(shù)學(xué)大神。

 
   你怎么可能贏得了莊家？

   論理性，沒(méi)有人能比賭場(chǎng)老板更理性。

 
   論數(shù)學(xué)，沒(méi)有人能比賭場(chǎng)老板請(qǐng)的專(zhuān)家更精通數(shù)學(xué)。

   論賭本，沒(méi)有人能比賭場(chǎng)老板的本錢(qián)更多。

   世上有太多人還在心存僥幸，告訴他唯一的答案。

 
   如果要想真正贏得人生這場(chǎng)賭局，法則只有一個(gè)：不賭。

 

 

---